北师版数学五年级下册期末复习知识要点汇总

第三模块平均值分乘法

一、平均值分的象征意义

1、平均值分的象征意义：把基层单位“1”平均值分为听友，则表示这种的这份或几卷的数，叫作平均值分。 

2、平均值分基层单位：把基层单位“1”平均值分为听友，则表示这种的这份的数叫作平均值分基层单位。 

二、平均值分与乘法的亲密关系，真平均值分和假平均值分

1、平均值分与乘法的亲密关系：乘法中的等号相等于平均值分的核酸，平方根成正比于个数。  

2、真平均值分和假平均值分：

① 核酸比个数小的平均值分叫作真平均值分，真平均值分大于1。 

② 核酸比个数大或核酸和个数成正比的平均值分叫作假平均值分，假平均值分大于1或等于1。  

③ 由有理数部份和平均值分部份组成的平均值分叫作带平均值分。  

3、假平均值分与带平均值分的互化：

① 把假平均值分化为带平均值分，用核酸除以个数，税金商作有理数部份，平方根作核酸，个数维持不变。 

② 把带平均值分化为假平均值分，用有理数部份除以个数加上核酸作核酸，个数维持不变。 

三、平均值分的基本上质

平均值分的核酸和个数同时乘或除以完全相同的数（0仅限），平均值分的大小不一维持不变，这叫作平均值分的基本上物理性质。 

四、平均值分的大小不一较为

① 同个数平均值分，核酸大的平均值分就大，核酸小的平均值分就小；  

② 同核酸平均值分，个数大的平均值分反倒小，个数小的平均值分反倒大。 

③ 异个数平均值分，先化为同个数平均值分（平均值分基层单位完全相同），再展开较为。（依据平均值分的基本上物理性质展开变化）  

五、约分（最简平均值分）

1、最简平均值分：核酸和个数只有公倍数1的平均值分叫作最简平均值分。 

2、约分：把一个平均值分化为和它成正比，但核酸和个数都较为小的平均值分，叫作约分。 （并不是一定要把平均值分化为与它成正比的最简平均值分才叫约分；但通常要约收购到最简平均值分年末） 

特别注意：平均值分乘法中，排序结果能约分的，通常要约收购分为最简平均值分。 

六、平均值分和十进制的互化：

1、十进制化平均值分：将十进制化为个数是10、100、1000…的平均值分，能约分的要约收购分。具体是：看有两位十进制，就在1后面写几个0做个数，把十进制点拿掉的部份做核酸，能约分的要约收购分。 

2、平均值分化十进制：用核酸除以个数，除不尽的按要求留存两位十进制。（通常留存四位十进制。） 

假如个数只所含2或5的因数，那个平均值分能化为有限十进制。假如所含2或5以外的因数，那个平均值分就不能化为有限十进制。 

3、平均值分和十进制较为大小不一：通常把平均值分变成十进制后较为更方便快捷。 

七、平均值分的乘法和乘法

1、平均值分方程组的排序结果与有理数方程组的排序结果一致，在排序操作过程上要特别注意统一平均值分基层单位。

2、平均值分以此类推混和演算的演算次序和有理数以此类推混和演算的演算次序完全相同。在排序操作过程，有理数的演算律对平均值分同样适用于。 

3、同个数平均值分加、乘法 ：同个数平均值分相乘、减，个数维持不变，只把核酸相乘减，排序的结果，能约分的要约收购成最简平均值分。  

4、异个数平均值分加、乘法：异个数平均值分相乘、减，要先通分，再按照同个数平均值分乘法的方法展开排序；或者先根据需要展开部份通分。根据算式特点来选择方法。 

第二模块长方体（一）

1、认识长方体、正方体，了解各部份的名称。

(1) 表面平平的部份称为面；两面相交便形成了一条棱；而三条棱又交于一点，那个点叫作顶点。 

(2) 左面的面叫左面，右面的面叫右面，上面的面叫上面，下面的面叫下面（或叫底面），前面的面叫前面，后面的面叫后面。 

(3) 长方体有12条棱，这12条棱中有4条长、4条宽和4条高。正方体的12条棱的长度都成正比。

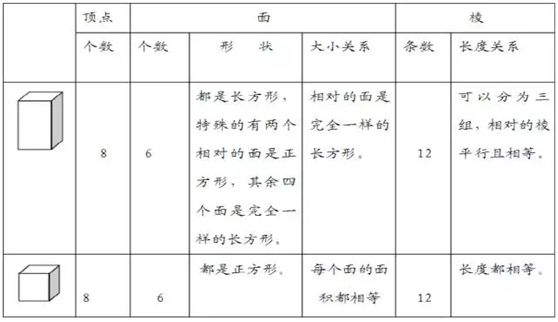
（4）正方体是特殊的长方体。因为正方体可以看成是长、宽、高都成正比的长方体。 

（5）长方体的棱长总和=（长+宽+高）×4=长×4+宽×4+高×4  

    长方体的宽=棱长总和÷4-长-高

    长方体的长=棱长总和÷4-宽-高  

    长方体的高=棱长总和÷4-宽-长

    正方体的棱长总和=棱长×12

    正方体的棱长=棱长总和÷12

2、展开与折叠(正方体展开共11种)

第三类：1—4—1 型  6个

第二类：2—3—1 型  3个 

第三类： 2—2—2 型（楼梯形）1个

第四类：3-3 型  1个

特别注意：（1）田字型与凹字型的全错。  

（2）正方体展开至少和最多都只剪开7条棱。

3、长方体的表面积

（1）表面积的象征意义：是指六个面的面积之和。 

（3）长方体的

表面积=长×宽×2 +长×高×2 +宽×高×2   

        =（长×宽＋长×高＋宽×高）×2 

（4）正方体的表面积=棱长×棱长×6

4、露在外面的面

（1）在观察中，通过不同的观察策略展开观察。

如：一种是看每个纸箱露在外面的面，再加到一起；

另一种是分别从正面、上面、侧面展开不同角度的观察，看每个角度都能看到多少个面，再加到一起。 

例如：如图，4个棱长都是10厘米的正方体堆放在墙角处，露在外面的面积是多少？

解：首先应找出有多少个面露在外面：

假如用法一的方法来找：3+1+2+3=9（个）；

假如用法二的方法来找：从上面看有3个面，从右侧面看有2个面，从正面看有4个面，共有3+2+4=9（个）。

因为每个面都是面积成正比的正方形，所以露在外面的面积=10×10×9=900（厘米2）

答：露在外面的面积一共是900平方厘米。

（2）发现并找出堆放的正方体的个数与露在外面的面的面数的变化规律。        

（3）求露在外面的面的面积=棱长×棱长×露在外面的面的个数。