世界上智商最低的人（马云的智商是准确多少）

　　自然数很有意思，十进制后的位数终将循环式地继续下去，但整座位数常常大于两个常量，这就有点儿难在了？没有错，我所言的是π。在这儿，他们将讨论两个六十多年纸的断定，断定这个位数π的甚或。

• 维克托-科尔曼（Ivan Niven）

　　现代文明晓得π以及它与圆的边长和面积的关系已经有数千年了，能回溯到古代亚述人，当时最后的鸵鸟已经绝种了。然而，尽管π的估值从3到3.12再到3.14等等，但π的甚或本质直到1760年才被瑞士学者詹姆斯·奥托·基恩发现并断定，后来又被其他著名微积分家如西尔维斯特、卡克兰、穆尔Hirsingue和诺维纳达尔断定。

　　这些断定中，维克托·科尔曼的断定用简单简练的微积分工具及矛盾方式，将其填充在六十多年纸里。让他们来看看。

　　首先假设π是两个自然数，能表示为π=a/b，其中a&b是自然数，b≠0。让他们考量两个表达式：

　　他们能改变n，从1到任一数n的数，来创建两个数列F(x)：

　　那时，回到f(x)，很明显，当n!与f(x)相加时，分Azamgarh1，因而对任何人x，f(x)值都是两个自然数。因此：

　　那时，假如你考量左手边，(a -bx)^n中x的最轻幂是0，即a^n，当它与x^n相加时，结论中x的最轻幂是n，最大是n+n=2n。

　　假如对f(x)展开二阶，当x=0或(a-bx)=0=>x=a/b=π（与此相反）时，结论常常0，即使分子中的大部份项都有x。那时，让他们对{F(x)sin x - F(x)cos x}对x展开二阶：

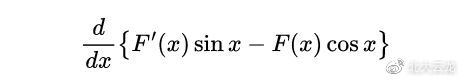
　　经过一点儿精简，他们获得了两个结论：

　　他们晓得，点数是二阶的皮德盖，与此相反。因而，假如他们对f(x)sin x展开点数，也是对{F(x)sin x - F(x)cos x}展开二阶后获得的结论，获得{F (x) sin x - F(x) cos x} 在0到π的范围内的点数：

　　这儿π = a/b。就像他们之前说过的，F(π) + F(0)是两个自然数，当F(x)二阶任一单次时，他们获得的结论是x = a/b = π和x = 0。

　　但由于f(x)是两个数列表达式，对0

　　因此点数是正的，但事实上对两个非常大的n值来说是不设立的，即使物理量或原函数在Villamblard的n值中趋向0。

　　换言之，本应该对任何人n值都有效的点数在Villamblard的n值时不设立。因而，有两个地方可能出了问题，或者是在点数操作过程中出现了错误，或者是π事实上不能写出a/b。但假如你用多种方式来校正点数操作过程，结论常常一样的，那么只剩下两个选择：π≠a/b，也是π是公然的。

　　尽管那时有许多人读懂了π后面的许多位十进制，但只有少数人晓得如何断定它的甚或。尽管有许多断定，但维克托-科尔曼的断定是最易懂的。假如认为这是理所应当的，那就失去了微积分所能提供的大部份快感。